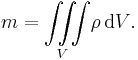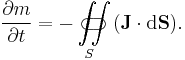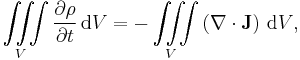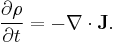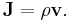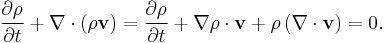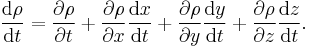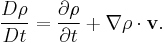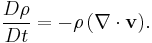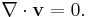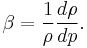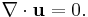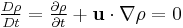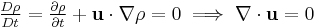Incompressible flow

In fluid mechanics or more generally continuum mechanics, incompressible (isochoric) flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid. An equivalent statement that implies incompressible flow is that the divergence of the fluid velocity is zero (see the derivation below, which illustrates why these conditions are equivalent).

Incompressible flow does not imply that the fluid itself is incompressible. It is shown in the derivation below that even compressible fluids can undergo incompressible flow. Incompressible fluids must have a constant density everywhere, while incompressible flow only requires that the density remain constant within a parcel of fluid which moves with the fluid velocity.

1 Derivation
2 Relation to compressibility
3 Relation to solenoidal field
4 Difference between incompressible flow and material
5 Related flow constraints
6 Numerical approximations of incompressible flow
7 References
8 See also

Derivation

The fundamental requirement for incompressible flow is that the density, $\rho$ , is constant within an infinitesimal volume, dV, which moves at the velocity of the fluid, v. Mathematically, this constraint implies that the material derivative (discussed below) of the density must vanish to ensure incompressible flow. Before introducing this constraint, we must apply the conservation of mass to generate the necessary relations. The mass is calculated by a volume integral of the density, $\rho$ :

${m} = {\iiint\limits_V\! \rho \,\mathrm{d}V}.$

The conservation of mass requires that the time derivative of the mass inside a control volume be equal to the mass flux, J, across its boundaries. Mathematically, we can represent this constraint in terms of a surface integral:

${\partial m \over \partial t} = {- \iint\limits_{S}\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset (\mathbf{J}\cdot \mathrm{d}\mathbf{S})}.$

The negative sign in the above expression ensures that outward flow results in a decrease in the mass with respect to time, using the convention that the surface area vector points outward. Now, using the divergence theorem we can derive the relationship between the flux and the partial time derivative of the density:

${\iiint\limits_V {\partial \rho \over \partial t} \,\mathrm{d}V} = {- \iiint\limits_V\left(\nabla\cdot\mathbf{J}\right) \, \mathrm{d}V},$

therefore:

${\partial \rho \over \partial t} = - \nabla \cdot \mathbf{J}.$

The partial derivative of the density with respect to time need not vanish to ensure incompressible flow. When we speak of the partial derivative of the density with respect to time, we are referring to this rate of change within a control volume of fixed position. By allowing the partial time derivative of the density to be non-zero, we are not restricting ourselves to incompressible fluids because the density is allowed to change as observed from a fixed position as fluid flows through the control volume. This approach maintains generality, and not requiring that the partial time derivative of the density vanishes illustrates that compressible fluids can still undergo incompressible flow. What we are interested in now is the change in density of a control volume which moves along with the fluid velocity, v. The flux is related to the fluid velocity through the following function:

${\mathbf{J}} = {\rho \mathbf{v}}.$

So that the conservation of mass implies that:

${\partial \rho \over \partial t} %2B {\nabla \cdot \left(\rho \mathbf{v} \right)} = {\partial \rho \over \partial t} %2B {\nabla \rho \cdot \mathbf{v}} %2B {\rho \left(\nabla \cdot \mathbf{v} \right)} = 0.$

The previous relation (where we have used the appropriate product rule) is known as the continuity equation. Now, we need the following relation about the total derivative of the density (where we apply the chain rule):

${\mathrm{d}\rho \over \mathrm{d}t} = {\partial \rho \over \partial t} %2B {\partial \rho \over \partial x} {\mathrm{d}x \over \mathrm{d}t} %2B {\partial \rho \over \partial y} {\mathrm{d}y \over \mathrm{d}t} %2B {\partial \rho \over \partial z} {\mathrm{d}z \over \mathrm{d}t}.$

So if we choose a control volume that is moving at the same rate as the fluid (i.e. (dx/dt, dy/dt, dz/dt) = v), then this expression simplifies to the material derivative:

${D \rho \over Dt} = {\partial \rho \over \partial t} %2B {\nabla \rho \cdot \mathbf{v}}.$

And so using the continuity equation derived above, we see that:

${D \rho \over Dt} = {- \rho \left(\nabla \cdot \mathbf{v} \right)}.$

A change in the density over time would imply that the fluid had either compressed or expanded (or that the mass contained in our constant volume, dV, had changed), which we have prohibited. We must then require that the material derivative of the density vanishes, and equivalently (for non-zero density) so must the divergence of the fluid velocity:

${\nabla \cdot \mathbf{v}} = 0.$

And so beginning with the conservation of mass and the constraint that the density within a moving volume of fluid remains constant, it has been shown that an equivalent condition required for incompressible flow is that the divergence of the fluid velocity vanishes.

Relation to compressibility

In some fields, a measure of the incompressibility of a flow is the change in density as a result of the pressure variations. This is best expressed in terms of the compressibility

$\beta = {\frac{1}{\rho}} {\frac{d\rho}{dp}}.$

If the compressibility is acceptably small, the flow is considered to be incompressible.

Relation to solenoidal field

An incompressible flow is described by a velocity field which is solenoidal. But a solenoidal field, besides having a zero divergence, also has the additional connotation of having non-zero curl (i.e., rotational component).

Otherwise, if an incompressible flow also has a curl of zero, so that it is also irrotational, then the velocity field is actually Laplacian.

Difference between incompressible flow and material

As defined earlier, an incompressible (isochoric) flow is the one in which

$\nabla \cdot \mathbf u = 0. \,$

This is equivalent to saying that

$\tfrac{D\rho}{Dt} = \tfrac{\partial \rho}{\partial t} %2B \mathbf u \cdot \nabla \rho = 0$

i.e. the material derivative of the density is zero. Thus if we follow a material element, its mass density will remain constant. Note that the material derivative consists of two terms. The first term 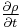$\tfrac{\partial \rho}{\partial t}$ describes how the density of the material element changes with time. This term is also known as the unsteady term. The second term, 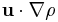$\mathbf u \cdot \nabla \rho$ describes the changes in the density as the material element moves from one point to another. This is the convection or the advection term. For a flow to be incompressible the sum of these terms should be zero.

On the other hand, a homogeneous, incompressible material is defined as one which has constant density throughout. For such a material, 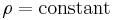$\rho = \text{constant}$ . This implies that,

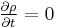$\tfrac{\partial \rho}{\partial t} = 0$ and

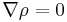$\nabla \rho = 0$ independently.

From the continuity equation it follows that

$\tfrac{D\rho}{Dt} = \tfrac{\partial \rho}{\partial t} %2B \mathbf u \cdot \nabla \rho = 0 \implies \nabla \cdot \mathbf u = 0$

Thus homogeneous materials always undergo flow that is incompressible, but the converse is not true.

It is common to find references where the author mentions incompressible flow and assumes that density is constant. Even though this is technically incorrect, it is an accepted practice. One of the advantages of using the incompressible material assumption over the incompressible flow assumption is in the momentum equation where the kinematic viscosity (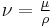 $\nu = \tfrac{\mu}{\rho}$ ) can be assumed to be constant. The subtlety above is frequently a source of confusion. Therefore many people prefer to refer explicitly to incompressible materials or isochoric flow when being descriptive about the mechanics.

Related flow constraints

In fluid dynamics, a flow is considered to be incompressible if the divergence of the velocity is zero. However, related formulations can sometimes be used, depending on the flow system to be modelled. Some versions are described below:

Incompressible flow: 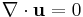${\nabla \cdot \mathbf u = 0}$ . This can assume either constant density (strict incompressible) or varying density flow. The varying density set accepts solutions involving small perturbations in density, pressure and/or temperature fields, and can allow for pressure stratification in the domain.
Anelastic flow: 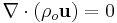${\nabla \cdot \left(\rho_{o}\mathbf u\right) = 0}$ . Principally used in the field of atmospheric sciences, the anelastic constraint extends incompressible flow validity to stratified density and/or temperature as well as pressure. This allows the thermodynamic variables to relax to an 'atmospheric' base state seen in the lower atmosphere when used in the field of meteorology, for example. This condition can also be used for various astrophysical systems.^[1]
Low Mach-number flow / Pseudo-incompressibility: 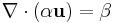$\nabla \cdot \left(\alpha \mathbf u \right) = \beta$ . The low Mach-number constraint can be derived from the compressible Euler equations using scale analysis of non-dimensional quantities. The restraint, like the previous in this section, allows for the removal of acoustic waves, but also allows for large perturbations in density and/or temperature. The assumption is that the flow remains within a Mach number limit (normally less than 0.3) for any solution using such a constraint to be valid. Again, in accordance with all incompressible flows the pressure deviation must be small in comparison to the pressure base state.^[2]

These methods make differing assumptions about the flow, but all take into account the general form of the constraint 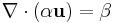$\nabla \cdot \left(\alpha \mathbf u \right) = \beta$ for general flow dependent functions $\alpha$ and $\beta$ .

Numerical approximations of incompressible flow

The stringent nature of the incompressible flow equations means that specific mathematical techniques have been devised to solve them. Some of these methods include:

The projection method (both approximate and exact)
Artificial compressibility technique (approximate)
Compressibility pre-conditioning

References

^ Durran, D.R. (1989). "Improving the Anelastic Approximation". Journal of the Atmospheric Sciences 46 (11): 1453–1461. Bibcode 1989JAtS...46.1453D. doi:10.1175/1520-0469(1989)046<1453:ITAA>2.0.CO;2. ISSN 1520-0469. http://ams.allenpress.com/archive/1520-0469/46/11/pdf/i1520-0469-46-11-1453.pdf.
^ Almgren, A.S.; Bell, J.B.; Rendleman, C.A.; Zingale, M. (2006). "Low Mach Number Modeling of Type Ia Supernovae. I. Hydrodynamics". Astrophysical Journal 637 (2): 922–936. arXiv:astro-ph/0509892. Bibcode 2006ApJ...637..922A. doi:10.1086/498426. http://seesar.lbl.gov/ccse/Publications/car/LowMachSNIa.pdf.